ОСНОВЫ ЭЛЕКТРОНИКИ

Конденсаторы и цепи переменного тока

1.13. RC - цепи: изменения во времени напряжения и тока

Для анализа цепей переменного тока (или в общем случае схем, работающих с изменяющимися напряжениями и токами) можно использовать характеристики двух типов. Во-первых, можно рассматривать изменения напряжения U и тока I во времени, а во-вторых - изменение амплитуды при изменении частоты сигнала. И те, и другие характеристики имеют свои преимущества, и в каждом практическом случае приходится выбирать наиболее подходящие. Мы начнем изучение цепей переменного тока с временных зависимостей, а в разд. 1.18 перейдем к частотным характеристикам.

Каковы же свойства схем, в состав которых входят конденсаторы? Для того чтобы ответить на этот вопрос, рассмотрим простейшую RC - цепь (рис. 1.29). Воспользуемся полученным ранее выражением для емкости:

C(dU/dt) = I = - U/R.

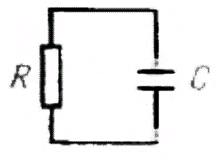
Рис. 1.29.

Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид:

U = Ae ^{- t/RC}.

Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис. 1.30.

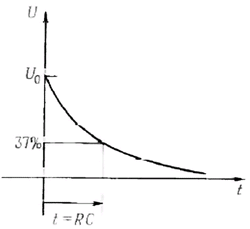
Рис. 1.30. Сигнал разряда RС - цепи.

Постоянная времени. Произведение RC называют постоянной времени цепи. Если R измерять в омах, а С - в фарадах, то произведение RC будет измеряться в секундах. Для конденсатора емкостью 1 мкФ, подключенного к резистору сопротивлением 1 кОм. постоянная времени составляет 1 мс, если конденсатор был предварительно заряжен и напряжение на нем составляет 1 В, то при подключении резистора в цепи появится ток, равный 1 мА.

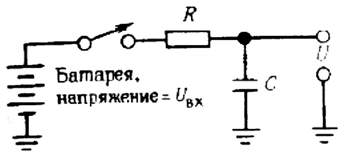
Рис. 1.31.

На рис. 1.31 показана несколько иная схема. В момент времени t = 0 схема подключается к батарее. Уравнение, описывающее работу такой схемы, выглядит следующим образом:

I = C(dU/dt) = (U_вх - U)/R.

и имеет решение

U = U_вх + Ae ^-t/RC.

Не пугайтесь, если не поняли, как выполнено математическое преобразование. Важно запомнить полученный результат. В дальнейшем мы будем многократно его использовать, не прибегая к математическим выкладкам. Постоянная величина А определяется из начальных условий (рис. 1.32): U = 0 при t = 0, откуда А = -U_вх и U = U_вх(1 - e ^-t/RC).

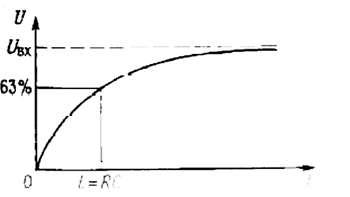
Рис. 1.32.

Установление равновесия. При условии t » RC напряжение достигает значения U_вх. (Советуем запомнить хорошее практическое правило, называемое правилом пяти RC. Оно гласит: за время, равное пяти постоянным времени, конденсатор заряжается или разряжается на 99%.) Если затем изменить входное напряжение U_вх (сделать его равным, например, нулю), то напряжение на конденсаторе U будет убывать, стремясь к новому значению по экспоненциальному закону e ^-t/RC. Например, если на вход подать прямоугольный сигнал U_вх, то сигнал на выходе U будет иметь форму, показанную на рис. 1.33.

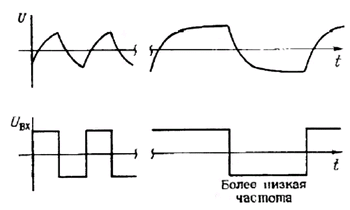
Рис. 1.33. Напряжение, снимаемое с конденсатора (верхние сигналы), при условии, что на него через резистор подается прямоугольный сигнал.

Упражнение 1.13. Докажите, что время нарастания сигнала (время, в течение которого сигнал изменяется от 10 до 90% своего максимального значения) составляет 2.2 RC.

У вас, наверное, возник вопрос: каков закон изменения для произвольного U^вх(t)? Для того чтобы ответить на него, нужно решить неоднородное дифференциальное уравнение (стандартные методы решения таких уравнений здесь не рассматриваются). В результате получим

U(t) = 1/RC ^t∫ _{- ∞}U_вхτe ^-t/RCdt.

Согласно полученному выражению, RC - цепь усредняет входное напряжение с коэффициентом пропорциональности e^-t/RC где Δt = τ - t. На практике, однако, такой вопрос возникает редко. Чаше всего рассматриваются частотные характеристики и определяют, какие изменения претерпевает каждая частотная составляющая входного сигнала. Скоро (разд. 1.18) мы также перейдем к этому немаловажную вопросу. А пока рассмотрим несколько интересных схем, хотя анализа которых достаточно временных зависимостей.

Упрощение с помощью эквивалентного преобразования Тевенина. Можно было бы приступить к анализу более сложных схем, пользуясь, как и раньше, методом решения дифференциальных уравнений. Однако чаше всего не стоит прибегать к решению дифференциальных уравнений. Большинство схем можно свести к RC - схеме. показанной на рис. 1.34. Пользуясь эквивалентным преобразованием для делителя напряжения, образованного резисторами R₁ и R₂, можно определить U(t) для скачка входного напряжения U_вх.

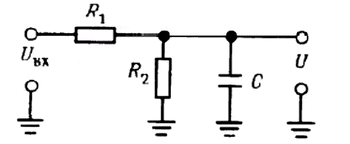
Рис. 1.34.

Упражнение 1.14. Для схемы, показанной на рис. 1.34. R₁ = R₂ = 10 кОм и С = 0,1 мкФ. Определите U(t) и изобразите полученную зависимость в виде графика.

Пример: схема задержки. Мы уже упоминали логические уровни - напряжения, определяющие работу цифровых схем. На рис. 1.35 показано, как с помощью конденсаторов можно получить задержанный импульс. В виде треугольников изображены КМОП - буферные усилители. Они дают высокий уровень на выходе (более половины величины напряжения питания постоянного тока) и наоборот. Первый буферный усилитель воспроизводит входной сигнал и обеспечивает небольшое выходное сопротивление, предотвращая тем самым воздействие на источник сигнала RС - цепи (вопрос о нагрузке схемы мы рассмотрели в разд. 1.05). Согласно характеристике RС - цепи, выходной сигнал для нее задерживается относительно входного, поэтому выходной буферный усилитель переключается на 10 мкc позже скачка напряжения на входе (напряжение на выходе RС - цепи достигает 50% своего максимального значения через 0,7 RC). На практике приходится принимать во внимание отклонение входного порога буфера от величины, равной половине напряжения питания, так как это отклонение изменяет задержку и ширину выходного импульса. Иногда подобную схему используют для того, чтобы задержать импульс на время, в течение которого может произойти какое-либо событие. При проектировании схем лучше не прибегать к подобным трюкам, но иногда они бывают полезны.

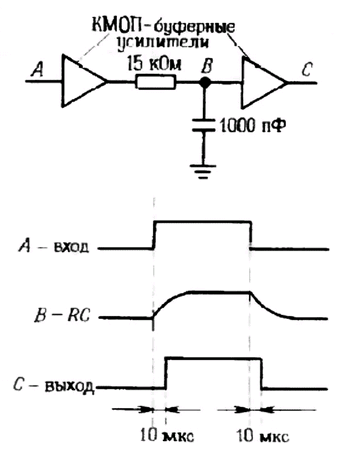
Рис. 1.35. Использование RС - цепи для формирования задержанного цифрового сигнала.

Индуктивности и трансформаторы