ОСНОВЫ ЭЛЕКТРОНИКИ

Полное и реактивное сопротивление

1.18. Частотный анализ реактивных схем

Для начала рассмотрим конденсатор, на который подается синусоидальное напряжение источника питания (рис. 1.47). Ток в схеме определяется следующим образом:

I(t) = C(dU/dt) = Cω (U₀ cosωt).

Из этого уравнения следует, что ток имеет амплитуду I и опережает входное напряжение по фазе на 90°. Если не принимать во внимание соотношение фаз, то

I = U/(1/ωC).

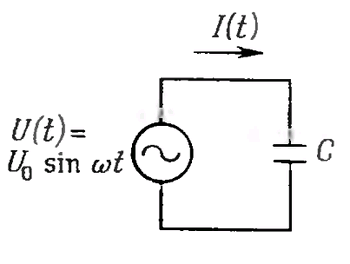
Рис. 1.47.

(Напомним, что ω = 2πf.) Конденсатор ведет себя как резистор, сопротивление которого зависит от частоты и определяется выражением R = 1/ωС, и, кроме того, ток, протекающий через конденсатор, сдвинут по фазе на 90° относительно напряжения (рис. 1.48). Например, через конденсатор емкостью 1 мкФ, подключенный к силовой сети с напряжением 110 В (эффективное значение) и частотой 60 Гц, будет протекать ток, эффективная амплитуда которого определяется следующим образом: I = 110/[1/2π · 60 · 10^-6)] = 41,5 мА (эффективное значение).

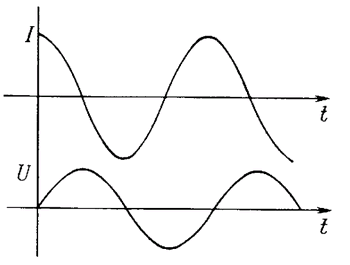
Рис. 1.48.

Замечание: сейчас нам необходимо воспользоваться комплексными переменными; при желании вы можете пропустить математические выкладки, приводимые в последующих разделах, и принять на веру полученные результаты (они выделены в тексте). Не думайте, что подробные алгебраические преобразования, приводимые в этих разделах, необходимы для понимания всего остального материала книги. Это не так - глубокое знание математики похвально, но совсем не обязательно. Следующий раздел, пожалуй, наиболее труден для тех, у кого нет достаточной математической подготовки. Но пусть это вас не огорчает.

Определение напряжения и тока с помощью комплексных чисел. Только что вы убедились в том. что в цепи переменного тока, работающей с синусоидальным сигналом некоторой частоты, возможен сдвиг по фазе между напряжением и током. Тем не менее если схема содержит только линейные элементы (резисторы, конденсаторы, индуктивности), то амплитуда токов на всех участках схемы пропорциональна амплитуде питающего напряжения. В связи с этим можно попытаться найти некоторые общие выражения тока, напряжения и сопротивления и обобщить тем самым закон Ома. Очевидно, что для того, чтобы определить ток в какой-либо точке схемы, недостаточно задать одно значение-дело в том, что ток характеризуется как амплитудой, так и сдвигом фазы.

Конечно, можно определять амплитуды и фазовые сдвиги напряжений и токов явно, например U(t) = 23,7sin(377t + 0,38), но оказывается, что проще это делать с помощью комплексных чисел. Вместо того чтобы тратить время и силы на сложение и вычитание синусоидальных функций, можно легко и просто складывать и вычитать комплексные числа. Так-как действующие значения напряжения и тока представляют собой реальные количественные величины, изменяющиеся во времени, следует вывести правило для перевода реальных количественных величин в комплексное представление и наоборот. Напомним еще раз, что мы имеем дело с частотой синусоидального колебания ω, и сформулируем следующие правила:

1. Напряжение и ток представляются комплексными величинами U и I. Напряжение U₀ cos (ωt + φ) представляется комплексным числом U₀e^jφ Напомним что e^jθ = cosθ + jsinθ, где j = √-1.

2. Для того чтобы получить выражение для действующего напряжения и тока. нужно умножить соответствующие комплексные представления на e^jωt и выделить действительную часть. Это записывается следующим образом: U (t) = Re (Ue^jωt), I(t) = Re (Ie^jωt). Иначе говоря.

(В электронике символ j используется вместо принятого в алгебре для комплексной переменной символа i, с тем чтобы избежать путаницы с током, который также обозначают символом i). Итак, в общем случае действующие напряжения и токи определяются следующим образом:

U(t) = Re(Ue^jωt) = Re (U) cosωt - Im (U) sinωt,

I(t) = Re(Ie^jωt) = Re (I) cosωt - Im (I) sinωt.

Например, комплексному напряжению U = 5j соответствует реальное напряжение

U (t) = Re [5j cosωt + 5j(j)sinωt] = 5sinωtB

Реактивное сопротивление конденсаторов и индуктивностей. Принятое соглашение позволяет применять закон Ома для схем, содержащих как резисторы, так и конденсаторы, и индуктивности. Определим реактивное сопротивление конденсатора и индуктивности. Нам известно, что U (t) = Re (U₀e^jωt). Так как в случае конденсатора справедливо выражение I = C(dU/dt) получим

I(t) = - U₀ Cωsinωt = Re[U₀e^jωt/(-j/ωC)] = Re(U₀e^jωt/X_c),

т.е. для конденсатора

X_c = -j/ωС,

X_c - это реактивное сопротивление конденсатора на частоте ω. Конденсатор емкостью 1 мкФ, например, имеет реактивное сопротивление - 2653j Ом на частоте 60 Гц и -0,16j Ом на частоте 1 МГц. Для постоянного тока реактивное сопротивление равно бесконечности.

Аналогичные рассуждения для индуктивности дают следующий результат: X_L = jωL.

Схема, содержащая только конденсаторы и индуктивности, всегда обладает мнимым импедансом: это значит, что напряжение и ток всегда сдвинуты по фазе друг относительно друга на 90° - схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть. Под реактивным сопротивлением подразумевается при этом только мнимая часть импеданса.

Обобщенный закон Ома. Соглашения, принятые для представления напряжений и токов, позволяют записать закон Ома в следующей простой форме:

I = U/Z, U = IZ,

означающей, что напряжение U, приложенное к схеме с импедансом Z, порождает ток I. Импеданс последовательно и параллельно соединенных элементов определяется по тем же правилам, что и сопротивление последовательно и параллельно соединенных резисторов:

Z = Z₁ + Z₂ + Z₃ + ...

(для последовательного соединения),

Z = 1/(1/Z₁ + 1/Z₂ + 1/Z₃ +...)

(для параллельного соединения).

И в заключение приведем формулы для определения импеданса резисторов, конденсаторов и индуктивностей:

Z_R = R (резистор),

Z_C = -j/ωС (конденсатор),

Z_L = j/ωL (индуктивность).

Полученные зависимости позволяют анализировать любые схемы переменного тока с помощью методов, принятых для схем постоянного тока, а именно с помощью закона Ома и формул для последовательного и параллельного соединения элементов. Результаты, которые мы получили при анализе таких схем, как, например, делитель напряжения, сохраняют почти такой же вид. Так же как и для схем постоянного тока, для сложных разветвленных схем переменного тока справедливы законы Кирхгофа: отличие состойт в том, что вместо токов I и напряжений U здесь следует использовать их комплексные представления: сумма падений напряжения (комплексного) в замкнутом контуре равна нулю; сумма токов (комплексных), втекающих в узел, равна сумме токов (комплексных), вытекающих из нею. Из последнего правила, как и в случае с цепями постоянного тока. вытекает, что ток (комплексный) в последовательной цепи всюду одинаков.

Упражнение 1.16. Используя формулы для импеданса параллельного и последовательного соединения эпементов, выведите формулы (разд. 1.12) для емкости двух конденсаторов, соединенных (а) параллельно, (б) последовательно. Подсказка: допустим, что в каждом случае конденсаторы имеют емкость С1, и С2. Запишите выражение для импеданса параллельно и поспеловательно соединенных элементов и приравняйте его импедансу конденсатора с емкостью С. Найдите С.

Попробуем воспользоваться рекомендованным методом для анализа простейшей цепи переменного тока, которая состоит из конденсатора, к которому приложено напряжение перменного тока. После того кратко остановимся на вопросе о мощности в реактивных схемах (это будет последний кирпич в фундаменте наших знаний) и рассмотрим простую, но очень полезную схему RC - фильтра.

Представим себе, что к силовой сети с напряжением 110В (эффективное значение) и частотой 60 Гц подключен конденсатор емкостью 1 мкФ. Какой ток протекает при этом через конденсатор? Воспользуемся обобщенным законом Ома: Z = -j/ωС. Следовательно, ток можно определить следующим образом: I = U/Z. Фаза напряжения произвольна, допустим U = А, т. е. U (t) = A cosωt, где амплитуда А = 110√2 ≈ 156 В, тогда I = jωCA ≈ 0,059 sinωt. Искомый ток имеет амплитуду 59 мА (эффективное значение составляет 41,5 мА) и опережает напряжение по фазе на 90°. Результат соответствует полученным ранее выводам. Отметим, что если бы нас интересовала только амплитуда тока, то можно было бы не прибегать к комплексным числам: если А = В/С, то А = В/С, где А, В, С - амплитуды комплексных чисел. То же самое справедливо и для произведения (см. упражнение 1.17). Для нашего случая I = U/Z = ωCU.

Иногда этот прием очень полезен.

Как ни странно, конденсатор в нашем примере мощность не рассеивает. Его подключение к сети не приводит к увеличению показаний счетчика электроэнергии. Разгадку этой «тайны» вы узнаете, прочитав следующий раздел. А затем мы продолжим анализ схем, содержащих резисторы и конденсаторы, с помошью обобщенного закона Ома.

Упражнение 1.17. Докажите, что если A = ВС, то А = ВС, где А, В, С-амплитуды комплексных чисел. Подсказка: представьте каждое комплексное число в форме А = Аe^jθ.

Мощность в реактивных схемах. Мгновенное значение мощности, потребляемой любым элементом схемы, определяется произведением Р = UI. Однако в реактивных схемах, где напряжение U и ток I связаны между собой не простой пропорциональной зависимостью, просто перемножить их нельзя. Дело в том, что могут возникать странные явления, например, знак произведения может изменяться в течение одного периода сигнала переменного тока. Такой пример показан на рис. 1.49. На интервалах А и С на конденсатор поступает некоторая мощность (правда, скорость ее изменения переменна), и благодаря этому он заряжается: накапливаемая конденсатором энергия увеличивается (мощность - это скорость изменения энергии). На интервалах В и D потребляемая мощность имеет отрицательный знак - конденсатор разряжается. Средняя мощность за период для нашего примера равна нулю; этим свойством обладают все реактивные элементы (индуктивности, конденсаторы и всевозможные их комбинации). Если вы знакомы с интегралами от тригонометрических функций, то следующее упражнение поможет вам доказать это свойство.

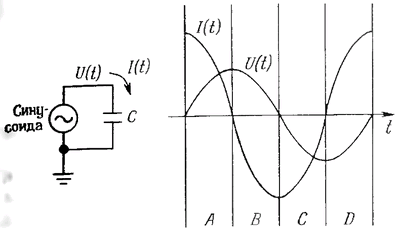
Рис. 1.49. При использовании синусоидального сигнала ток через конденсатор опережает напряжение по фазе на 90°.

Упражнение 1.18. (дополнительное). Докажите, что схема в среднем за полный период не потребляет мощности, если протекающий через нее ток сдвинут по фазе относительно питающего напряжения на 90°.

Как определить среднюю потребляемую мощность для произвольной схемы? В общем случае можно просуммировать произведения UI и разделить сумму на длительность истекшего интервала времени. Иными словами.

P = 1/T ^T∫₀U(t)I(t)dt,

где Т - полный период времени. Практически так мощность почти никогда не определяют. Нетрудно доказать, что средняя мощность определяется следующим выражением:

P = Re(U^*I) = Re(UI^*),

где U и I - эффективные комплексные значения напряжения и тока.

Рассмотрим пример. Допустим, что в предыдущей схеме конденсатор питается синусоидальным напряжением, эффективное значение которого равно 1 В. Для простоты будем выполнять все преобразования с эффективными значениями. Итак: U = 1, I = U/(j/ωC), Р = Re [UI^*] = Re (jωC) = 0. Мы получили, что средняя мощность, как и утверждалось, равна нулю.

А теперь рассмотрим схему, показанную на рис. 1.50. Выполним ряд преобразований:

Z = R-j/ωC.

U = U₀,

I = U/Z = U₀/[R + (j/ωC)]/[R² + (1/ω²C²)],

P = Re (UI^*) = U₀² R/[R² + (1/ω²C²)].

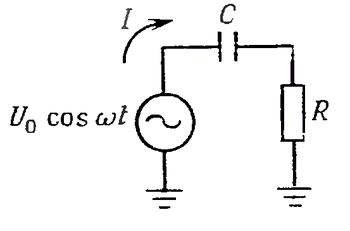
Рис. 1.50.

В третьей строке преобразований при определении тока I мы умножили числитель и знаменатель на комплексное число, сопряженное знаменателю, для того чтобы получить в знаменателе действительное число. Полученная величина меньше, чем произведение амплитуд U и I; ее отношение к этому произведению называют коэффициентом мощности:

|U||I| = U₀²/[R² + (1/ω²C²)]^1/2,

Коэффициент мощности - это косинус угла, определяющего сдвиг фаз напряжения и тока, он лежит в диапазоне от 0 (для реактивной схемы) до 1 (для резистивной схемы). Если коэффициент мощности меньше 1, то это значит, что в схеме присутствует реактивный элемент.

Упражнение 1.19. Докажите, что вся средняя мощность предыдущей схемы рассеивается на резисторе. Для того, чтобы решить эту задачу, нужно определить величину отношения U_R²/R. Определите, чему будет равна эта мощность в ваттах, если цепь, состоящая из последовательно соединенных конденсатора емкостью 1 мкФ и резистора сопротивлением 1 кОм, подключена к силовой сети с эффективным напряжением 110 В (частота 60 Гц).

Коэффициент мощности играет немаловажную роль в распределении больших мощностей, так как реактивные токи не передают нагрузке никакой полезной мощности, зато вызывают нагрев в сопротивлениях проводов генераторов и трансформаторов (температура нагрева пропорциональна I²R). Бытовые потребители электроэнергии платят только за «действительную» потребляемую мощность [Re(UI^*)], а промышленные потребители - с учетом коэффициента мощности. Вот почему большие предприятия для погашения влияния индуктивных реактивных сопротивлений производственного оборудования (моторов) сооружают специальные конденсаторные блоки.

Упражнение 1.20. Покажите, что последовательное подключение конденсатора емкостью С = l/ω²L к последовательной RL цепи делает коэффициент мощности этой цепи равным единице. Затем рассмотрите параллельную цепь и параллельно подключенный конденсатор.

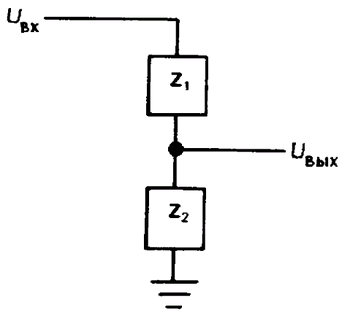
Рис. 1.51. Обобщенная схема делителя напряжения: пара электрических цепей с произвольным импедансом.

Делители напряжения: обобщение. Простейший делитель напряжения (рис. 1.5) состоит из пары последовательно соединенных резисторов. Входное напряжение измеряется в верхней точке относительно земли, а выходное-в точке соединения резисторов относительно земли. От простейшего резистивного делителя перейдем к более общей схеме делителя, если один или оба резистора заменим на конденсатор или индуктивность, как на рис. 1.51 (в более сложной схеме присутствуют и R и L и С). Вообще говоря, в таком делителе отношение U_вых/U_вх не является постоянной величиной, а зависит от частоты. Анализ схемы выполняется без всяких хитроумных приемов:

I = U_вх/Z_полн,

Z_полн = Z₁ + Z₂,

U_вых = Z2 = U_вх[Z₂/(Z₁ + Z₂)].

Не будем сосредоточивать внимание на полученном результате, рассмотрим лучше некоторые простые, но очень важные примеры.

Диоды и диодные схемы