Полное и реактивное сопротивление
1.20. Векторные диаграммы
Для анализа реактивных схем очень удобен один графический метод. В качестве примера рассмотрим тот факт, что RС - фильтр на частоте ƒ = 1/2πRC обеспечивает ослабление на 3 дБ. Этот результат мы получили в разд. 1.19. Он справедлив как для фильтров высоких частот, так и для фильтров низких частот. На первый взгляд этот факт может показаться странным, так как на этой частоте реактивное сопротивление конденсатора равно сопротивлению резистора и можно предположить, что ослабление должно составлять 6 дБ. К такому же результату вы придете, если замените конденсатор резистором с таким же, как у конденсатора, импедансом (напомним, что ослабление 6 дБ означает уменьшение напряжения вдвое). Дело в том, что нужно учитывать реактивность конденсатора. И в этом как раз может помочь векторная диаграмма (рис. 1.61). Вдоль осей откладываются действительная (активная или резистивная) и мнимая (реактивная или емкостная) компоненты импеданса. На такой же плоскости можно изображать напряжение (комплексное) в последовательных цепях подобного типа, так как ток в такой цепи во всех точках одинаков. Итак, в нашей схеме (будем рассматривать ее в качестве RС - делителя напряжения) входное напряжение (приложенное к последовательному соединению резистора R и конденсатора С) пропорционально длине гипотенузы, а выходное напряжение (снимаемое с резистора R) - длине стороны R треугольника. Диаграмма соответствует такой частоте, при которой модуль реактивного сопротивления конденсатора равен R, т.е. ƒ = 1/2πRC. Из диаграммы видно, что отношение выходного напряжения ко входному составляет 1/√2 т.е. -ЗдБ.
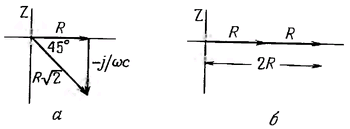
Рис. 1.61.
Угол между векторами определяет фазовый сдвиг между входным и выходным напряжением. Например, в точке 3 дБ выходная амплитуда равна входной, поделенной на √2, а сам выходной сигнал опережает входной по фазе на 45°. Графический метод дает наглядное представление о величинах амплитуд и соотношении фаз в RLC - цепях. Например, с помощью этого метода можно определить характеристику фильтра высоких частот, которую мы уже получили раньше с помощью алгебраических преобразований.
Упражнение 1.23. Пользуясь методом векторной диаграммы, получите характеристику RС - фильтра высоких частот:
Uвых = R/[R2 + (1/ω2C2)]1/2 Uвх.
Упражнение 1.24. На какой частоте ослабление RС-фильтра низких частот будет равно 6 дБ (выходное напряжение равно половине входного)? Чему равен фазовый сдвиг на этой частоте?
Упражнение 1.25. Пользуясь методом векторной диаграммы, получите характеристику фильтра низких частот, выведенную выше алгебраическим путем.
В следующей главе (разд. 2.08) приводится интересный пример использования векторной диаграммы для построения фазосдвигающей схемы, дающей постоянную амплитуду.