Полное и реактивное сопротивление
1.22. Резонансные схемы и активные фильтры
Конденсаторы, которые используются в специальных схемах, называемых активными фильтрами, а также в сочетании с индуктивностями, позволяют «заострять» частотную характеристику схемы (по сравнению с пологой характеристикой RС - фильтра характеристика такой схемы на некоторой частоте имеет большой резкий всплеск). Подобные схемы находят применение в устройствах, работающих в диапазоне звуковых частот и радиочастот. Итак, познакомимся с LC - цепями (подробному анализу этих цепей и активных фильтров посвящены гл. 5).
Начнем со схемы, представленной на рис. 1.62. На частоте ƒ реактивное сопротивление LC - контура равно
1/ZLC = 1/ZC + 1/ZL = 1/jωL - ωC/j = j(ωC - 1/ωL),
или ZLC = j/[(1/ωL) - ωC].
LC-контур в сочетании с резистором R образует делитель напряжения; в связи с тем, что индуктивность и конденсатор противоположным образом реагируют на изменение частоты, импеданс параллельной LC - цепи на резонансной частоте ƒ0 = 1/2π(LC)1/2 стремится к бесконечности на характеристике при этом значении частоты должен наблюдаться резкий всплеск. График такой характеристики представлен на рис. 1.63.
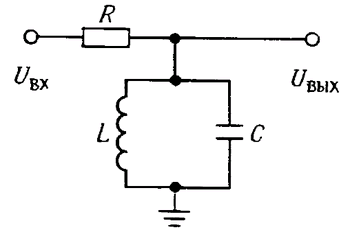
Рис. 1.62. Резонансная LC-схема: широкополосный фильтр.
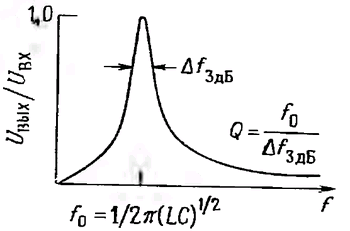
Рис. 1.63.
В действительности пик характеристики сглажен за счет потерь в индуктивности и конденсаторе, однако если схема сконструирована хорошо, то эти потери очень невелики. Если же хотят специально сгладить характеристику, то в схему включают дополнительный резистор, ухудшающий добротность контура Q. Такая схема называется параллельным резонансным LC - контуром или избирательной схемой. Она широко используется в радиотехнике для выделения из всего частотного диапазона сигналов некоторой частоты усиления (L или С могут быть переменными, и с их помощью можно настраивать резонансный контур на определенную частоту). Чем выше импеданс источника, тем острее пик характеристики; как вы вскоре убедитесь, в качестве источника принято использовать устройство типа источника тока. Коэффициент добротности Q позволяет оценивать характеристику контура: чем больше добротность, тем острее характеристика. Добротность равна резонансной частоте, поделенной на ширину пика, определенную по точкам -3 дБ. Для параллельной RLC - схемы Q = ω0RC.
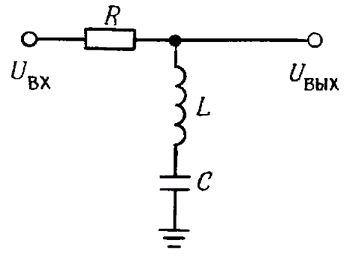
Рис. 1.64. Узкополосный режекторный LC - фильтр («ловушка»).
Другой разновидностью LC - схем является последовательная LC - схема (рис. 1.64). Используя выражение для импеданса, можно показать, что импеданс последовательной LC - схемы стремится к нулю на частоте ƒ0 = 1/2π(LC)1/2; такая схема на резонансной частоте или вблизи нее как бы «захватывает» сигнал и заземляет его. Эта схема, так же как и предыдущая, применяется в основном в радиотехнике. На рис. 1.65 изображена ее характеристика. Для последовательной RLC-схемы Q = ω0L/R.
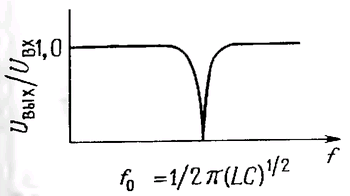
Рис. 1.65.
Упражнение 1.26. Выведите выражение для характеристики (определяющей зависимость отношения Uвых / Uвх от частоты) схемы с последовательным LC - контуром, показанной на рис. 1.64.