5.03. Введение в активные фильтры: обзор
При использовании в качестве элемента схемы фильтра ОУ можно синтезировать характеристику любого RLC-филътра без применения катушек индуктивности. Такие безиндуктивные фильтры известны под названием «активные фильтры» из-за наличия в их схеме активного элемента (усилителя).
Активные фильтры можно использовать для реализации фильтров нижних и верхних частот полосовых и полосноподавляющих фильтров, выбирая тип фильтра в зависимости о наиболее важных свойств характеристики, таких, как максимальная равномерность усиления в полосе пропускания крутизна переходной области или независимость времени запаздывания от частоты (далее об этом подробнее). Кроме того, можно построить как «всепропускающие фильтры» с плоской амплитудно-частотной характеристикой, но нестандартной фазочастотной характеристикой (они также известны как «фазовые корректоры»), так и наоборот - фильтр с постоянным фазовым сдвигом, но с произвольной амплитудно-частотной характеристикой.
Конвертеры отрицательного полного сопротивления и гираторы. Есть два интересных схемных элемента, которые следует упомянуть в любом обзоре: это - конвертер отрицательного полного сопротивления (КОС) и гиратор. Эти устройства могут имитировать свойства катушек индуктивности, хотя в них кроме ОУ используются только конденсаторы и резисторы.
Раз это так, то мы можем делать безиндуктивные фильтры с идеальными свойствами RLC - фильтра, таким образом - это по крайней мере один из способов реализации активных фильтров.
КОС преобразует полное сопротивление в ему противоположное (т. е. с обратным знаком), в то время как гиратор преобразует полное сопротивление в обратное (т.е. емкость в индуктивность). Следующие упражнения помогут уяснить, как это происходит.
Упражнение 5.1. Покажите, что изображенная на рис. 5.4 схема представляет собой конвертер полного сопротивления, в частности что Zвх = - Z. Подсказка: подайте на вход какое-нибудь напряжение U и вычислите входной ток I. Затем возьмите их отношение, чтобы найти Zвх = U/I.
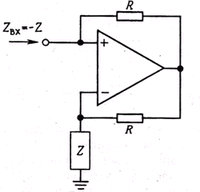
Рис. 5.4. Преобразователь (конвертер) полного отрицательного сопротивления.
Упражнение 5.2. Покажите, что схема на рис. 5.5 есть гиратор, в частности что Zвх = R2/Z. Подсказка: эту схему можно рассматривать как набор делителей напряжения, начиная справа. Таким образом, КОС превращает конденсатор в «обратную» катушку индуктивности:
Zc = 1/jωC -> Zвх = j/ωC,
т.е. в том смысле, что порождаемый ток запаздывает относительно приложенного напряжения, а его полное сопротивление имеет неправильную частотную зависимость (при возрастании частоты оно не растет, а убывает). Гиратор же, напротив, превращает конденсатор в элемент с истинной индуктивностью:
Zc = 1/jωC -> Zвх = j/ωCR2,
т.е. индуктивность которого L = CR2.
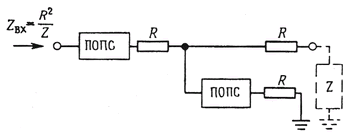
Рис. 5.5.
Существование гиратора делает интуитивно ясным тот факт, что можно построить безындуктивный фильтр, имитирующий любой фильтр, использующий катушки индуктивности: просто заменить каждую катушку «гиратированным» конденсатором. Такое применение гираторов вполне корректно, и ранее упомянутый телефонный фильтр построен именно таким способом. Кроме того, простая вставка гираторов в существующие RLC-схемы позволяет создавать много иных структур фильтров. Проектирование активных безындуктивных фильтров - весьма активно развивающаяся область, и описания новых конструкций появляются в журналах каждый месяц.
Фильтры Саллена и Ки. На рис. 5.6 приведен пример простого фильтра, построенного даже отчасти из интуитивных соображений. Он известен как фильтр Саллена и Ки, по имени его изобретателей. Здесь в качестве усилителя с единичным коэффициентом усиления может использоваться ОУ, включенный в режиме повторителя, либо просто эмиттерный повторитель. Данный фильтр представляет собой двухполюсный фильтр верхних частот. Следует отметить, что это был бы просто двухкаскадный RС-фильтр, если бы первый резистор не был соединен выходом. Легко показать, что на очень низких частотах наклон характеристик такой же, как и у RС-фильтра, поскольку выходной сигнал практически равен нулю. Рост же выходного сигнала при увеличении его частоты приводит к уменьшению ослабления в результате действия этой следящей связи, и за счет этого становится более резким излом характеристики. Конечно, такое объяснение на пальцах не может заменить полного расчета, уже, к счастью, проделанного для огромного числа хороших фильтров. Мы вернемся к схемам активных фильтров в разд. 5.06.
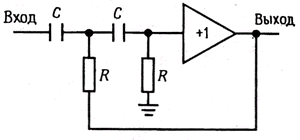
Рис. 5.6.