5.05. Типы фильтров
При анализе фильтров и при расчете их параметров всегда используются некоторые стандартные термины и имеет смысл придерживаться их с самого начала.
Предположим, что требуется фильтр нижних частот с плоской характеристикой в полосе пропускания и резким переходом к полосе подавления. Окончательный же наклон характеристики в полосе задерживания всегда будет 6n дБ/октава, где n - число «полюсов». На каждый полюс необходим один конденсатор (или катушка индуктивности), поэтому требования к окончательной скорости спада частотной характеристики фильтра, грубо говоря, определяют его сложность.
Теперь предположим, что вы решили использовать 6-полюсный фильтр нижних частот. Вам гарантирован окончательный спад характеристики на высоких частотах 36 дБ/октава. В свою очередь теперь можно оптимизировать схему фильтра в смысле обеспечения максимально плоской характеристики в полосе пропускания за счет уменьшения крутизны перехода от полосы пропускания к полосе задерживания. С другой стороны, допуская некоторую неравномерность характеристики в полосе пропускания, можно добиться более крутого перехода от полосы пропускания к полосе задерживания. Третий критерий, который может оказаться важным, описывает способность фильтра пропускать сигналы со спектром, лежащим в полосе пропускания, без искажений их формы, вызываемых фазовыми сдвигами. Можно также интересоваться временем нарастания, выбросом и временем установления.
Известны методы проектирования фильтров, пригодные для оптимизации любой из этих характеристик или их комбинаций. Действительно разумный выбор фильтра происходит не так, как описано выше; как правило, сначала задаются требуемая равномерность характеристики в полосе пропускания и необходимое затухание на некоторой частоте вне полосы пропускания и другие параметры. После этого выбирается наиболее подходящая схема с количеством полюсов, достаточным для того, чтобы удовлетворялись все эти требования. В следующих нескольких разделах будут рассмотрены три наиболее популярных типа фильтров, а именно фильтр Баттерворта (максимально плоская характеристика в полосе пропускания), фильтр Чебышева (наиболее крутой переход от полосы пропускания к полосе подавления) и фильтр Бесселя (максимально плоская характеристика времени запаздывания). Любой из этих типов фильтров можно реализовать с помощью различных схем фильтров; некоторые из них мы обсудим позже Все они равным образом годятся для построения фильтров нижних и верхних частот и полосовых фильтров.
Фильтры Баттерворта и Чебышева. Фильтр Баттерворта обеспечивает наиболее плоскую характеристику в полосе пропускания, что достигается ценой плавности характеристики в переходной области т.е. между полосами пропускания и задерживания. Как будет показано дальше у него также плохая фазочастотная характеристика. Его амплитудно-частотная характеристика задается следующей формулой:
Uвых/Uвх = 1/[1 + (ƒ/ƒc)2n]1/2,
где n определяет порядок фильтра (число полюсов). Увеличение числа полюсов дает возможность сделать более плоским участок характеристики в полосе пропускания и увеличить крутизну спада от полосы пропускания к полосе подавления, как это показано на рис. 5.10.
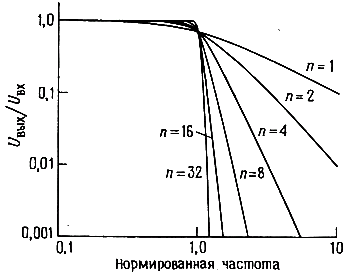
Рис. 5.10 Нормированные характеристики фильтров нижних частот Баттерворта. Обратите внимание увеличение крутизны спада характеристики с увеличением порядка фильтра.
Выбирая фильтр Баттерворта, мы ради максимально плоской характеристики поступаемся всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза ƒс - эта частота обычно соответствует точке -3 дБ.
В большинстве применений самым существенным обстоятельством является то, что неравномерность характеристики в полосе пропускания не должна превышать некоторой определенной величины, скажем 1 дБ. Фильтр Чебышева отвечает этому требованию, при этом допускается некоторая неравномерность характерности во всей полосе пропускания, но при этом сильно увеличивается острота ее излома. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. Допуская увеличение неравномерности в полосе пропускания, получаем более острый излом. Амплитудно-частотная характеристика этого фильтра задается следующим соотношением
Uвых/Uвх = 1/[1 + ε2Cn2(ƒ/ƒc)]1/2,
где Сn- полином Чебышева первого рода степени n, а ε - константа, определяющая неравномерность характеристики в полосе пропускания. Фильтр Чебышева, как и фильтр Баттерворта имеет фазочастотные характеристики, далекие от идеальных. На рис. 5.11 представлены для сравнения характеристики 6-полюсных фильтров нижних частот Чебышева и Баттерворта. Как легко заметить, и тот, и другой намного лучше 6-полюсного RC-фильтра.
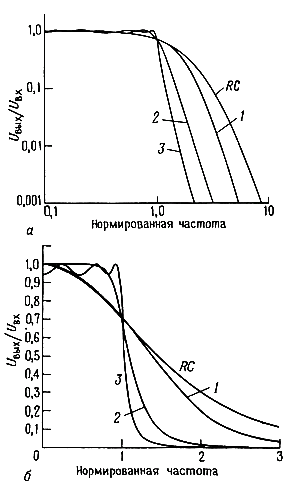
Рис. 5.11. Сравнение характеристик некоторых обычно применяемых 6-полюсных фильтров нижних частот. Характеристики одних и тех же фильтров изображены и в логарифмическом (вверху), и в линейном (внизу) масштабе. 1 - фильтр Бесселя; 2 - фильтр Баттерворта; 3 - фильтр Чебышева (пульсации 0,5 дБ).
На самом деле фильтр Баттерворта с максимально плоской характеристикой в полосе пропускания не столь привлекателен, как это может показаться, поскольку в любом случае приходится мириться с некоторой неравномерностью в полосе пропускания (для фильтра Баттерворта это будет постепенное понижение характеристики при приближении к частоте ƒс, а для фильтра Чебышева-пульсации, распределенные по всей полосе пропускания). Кроме того, активные фильтры, построенные из элементов, номиналы которых имеют некоторый допуск, будут обладать характеристикой, отличающейся от расчетной, а это значит, что в действительности на характеристике фильтра Баттерворта всегда будет иметь место некоторая неравномерность в полосе пропускания. На рис. 5.12 проиллюстрировано влияние наиболее нежелательных отклонений значений емкости конденсатора и сопротивления резистора на характеристику фильтра.
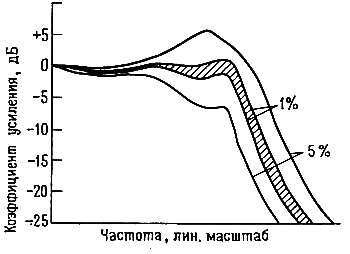
Рис. 5.12. Влияние изменений параметров элементов на характеристику активного фильтра.
В свете вышеизложенного весьма рациональной структурой является фильтр Чебышева. Иногда его называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что по полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1 дБ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в переходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием 20 дБ на частоте, отличающейся на 25% от граничной частоты полосы пропускания. Расчет показывает, что в этом случае требуется 19-полюсный фильтр Баттерворта или всего лишь 8-полюсный фильтр Чебышева.
Мысль о том, что можно мириться с пульсациями характеристики в полосе пропускания ради увеличения крутизны переходного участка, доводится до своего логического завершения в идее так называемого эллиптического фильтра (или фильтра Кауэра), в котором допускаются пульсации характеристики как в полосе пропускания, так и в полосе задерживания ради обеспечения крутизны переходного участка даже большей, чем у характеристики фильтра Чебышева. С помощью ЭВМ можно сконструировать эллиптические фильтры так же просто, как и классические фильтры Чебышева и Баттерворта. На рис. 5.13 представлено графическое задание амплитудно-частотной характеристики фильтра. В этом случае (фильтр нижних частот) определяются допустимый диапазон коэффициента передачи фильтра (т.е. неравномерность) в полосе пропускания, минимальная частота, на которой характеристика покидает полосу пропускания, максимальная частота, где характеристика переходит в полосу задерживания, и минимальное затухание в полосе задерживания.
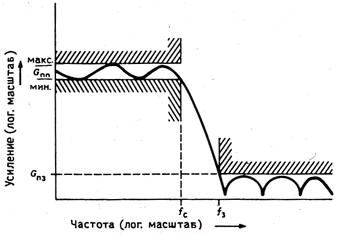
Рис. 5.13. Задание параметров частотной характеристики фильтра.
Фильтры Бесселя. Как было установлено ранее, амплитудно-частотная характеристика фильтра не дает о нем полной информации. Фильтр с плоской амплитудно-частотной характеристикой может иметь большие сдвиги фаз. В результате этого форма сигнала, спектр которого лежит в полосе пропускания, будет искажена при прохождении через фильтр. В ситуации, при которой форма сигнала имеет первостепенное значение, желательно иметь в распоряжении линейно-фазовый фильтр (фильтр с постоянным временем запаздывания). Предъявление к фильтру требования обеспечения линейного изменения сдвига фазы в зависимости от частоты эквивалентно требованию постоянства времени запаздывания для сигнала, спектр которого расположен в полосе пропускания, т. е. отсутствия искажений формы сигнала. Фильтр Бесселя (также называемый фильтром Томсона) имеет наиболее плоский участок кривой времени запаздывания в полосе пропускания, подобно тому как фильтр Баттерворта имеет наиболее плоскую амплитудно-частотную характеристику. Чтобы понять, какое улучшение во временной области дает фильтр Бесселя, посмотрите на рис. 5.14, где изображены нормированные по частоте графики времени запаздывания для 6-полюсных фильтров нижних частот Бесселя и Баттерворта. Плохая характеристика времени запаздывания фильтра Баттерворта обуславливает появление эффектов типа выброса при прохождении через фильтр импульсных сигналов. С другой же стороны, за постоянство времен запаздывания у фильтра Бесселя приходится расплачиваться тем, что его амплитудно-частотная характеристика имеет еще более пологий переходной участок между полосами пропускания и задерживания, чем даже у характеристики фильтра Баттерворта.
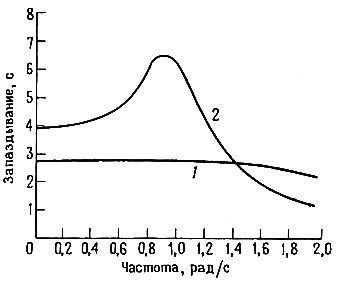
Рис. 5.14. Сравнение временных запаздываний для 6-полосных фильтров нижних частот Бесселя (1) и Баттерворта (2). Фильтр Бесселя благодаря своим превосходным свойствам во временной области дает наименьшее искажение формы сигнала.
Существует много различных способов проектирования фильтров, в которых делаются попытки улучшить рабочие параметры фильтра Бесселя во временной области, частично жертвуя постоянством времени запаздывания ради уменьшения времени нарастания и улучшения амплитудно-частотной характеристики. Фильтр Гаусса имеет почти столь же хорошие фазочастотные характеристики, как и фильтр Бесселя, но при улучшенной переходной характеристике. Другой интересный класс представляют собой фильтры, позволяющие добиться одинаковых по величине пульсаций кривой времени запаздывания в полосе пропускания (аналогично пульсациям амплитудно-частотной характеристики фильтра Чебышева) и обеспечивающие примерно одинаковое запаздывание для сигналов со спектром вплоть до полосы задерживания. Еще один подход к созданию фильтров с постоянным временем запаздывания - это применение всепропускающих фильтров, называемых иначе корректорами во временной области. Эти фильтры обладают постоянной амплитудно-частотной характеристикой, а сдвиг фазы может меняться согласно конкретным требованиям. Таким образом, их можно применять для выравнивания времени запаздывания любых фильтров, в частности фильтров Баттерворта и Чебышева.
Сравнение фильтров. Несмотря на ранее высказанные замечания о переходной характеристике фильтров Бесселя, он все же обладает очень хорошими свойствами во временной области по сравнению с фильтрами Баттерворта и Чебышева. Сам фильтр Чебышева при его весьма подходящей амплитудно-частотной характеристике имеет наихудшие параметры во временной области из всех этих трех типов фильтров. Фильтр Баттерворта дает компромисс между частотами и временными характеристиками. На рис. 5.15 дана информация по рабочим характеристикам этих трех типов фильтров во временной области, дополняющая приведенные ранее графики амплитудно-частотных характеристик. По этим данным можно сделать вывод, что в тех случаях, когда важны параметры фильтра во временной области, желательно применять фильтр Бесселя.
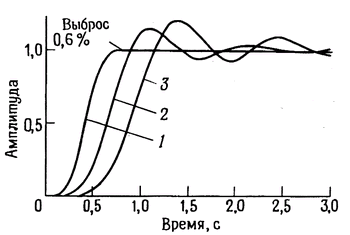
Рис. 5.15. Сравнение переходных процессов 6-полюсных фильтров нижних частот. Кривые нормированы приведением значения ослабления 3 дБ к частоте 1 Гц. 1 - фильтр Бесселя; 2 - фильтр Баттерворта; 3 - фильтр Чебышева (пульсации 0.5 дБ).