Активные фильтры и генераторы

Схемы активных фильтров

5.07. Проектирование фильтров на ИНУН с использованием наших упрощенных таблиц

Перед тем как пользоваться табл. 5.2, надо решить, какая характеристика фильтра нам нужна. Как уже говорилось ранее, фильтр Баттерворта хорош, если нужна максимально плоская характеристика в полосе пропускания, фильтр Чебышева обеспечивает наиболее крутой спад от полосы пропускания к полосе задерживания (ценой некоторой неравномерности характеристики в полосе пропускания), а фильтр Бесселя имеет наилучшую фазо-частотную характеристику, т.е. постоянное запаздывание сигнала в полосе пропускания и соответственно хорошую переходную характеристику. Амплитудно-частотные характеристики всех этих типов даны на соответствующих графиках (рис. 5.17).

Таблица 5.2 ИНУН - фильтры нижних частот

	Фильтр Баттерворта	Фильтр Бесселя		Фильтр Чебышева (0.5Дб)		Фильтр Чебышева (0.2Дб)
	K	ƒн	K	ƒн	K	ƒн	K
2	1.586	1.274	1.268	1.231	1.842	0.907	2.114
4	1.152	1.432	1.084	0.597	1.582	0.471	1.924
	2.235	1.606	1.759	1.031	2.660	0.964	2.782
6	1.068	1.607	1.040	0.396	1.537	0.316	1.891
	1.586	1.692	1.364	0.768	2.448	0.730	2.648
	2.483	1.908	2.023	1.011	2.846	0.983	2.904
8	1.038	1.781	1.024	0.297	1.522	0.238	1.879
	1.337	1.835	1.213	0.599	2.379	0.572	2.605
	1.889	1.956	1.593	0.861	2.711	0.842	2.821
	2.610	2.192	2.184	1.006	2.913	0.990	2.946

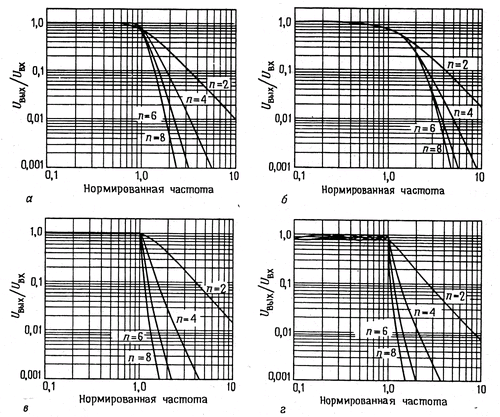
Pиc. 5.17. Графики нормированных частотных характеристик 2 - , 4 - , 6 - и 8 - полюсных фильтров из табл. 5.2. Характеристики фильтров Баттерворта (а) и Бесселя (б) нормированы приведением ослабления 3 дБ к единичной частоте, а фильтры Чебышева - приведением к этой частоте ослабления 0,5 дБ (в) и 2 дБ (г) соответственно.

Для конструирования n-полюсного фильтра (при четном n) нужно соединить каскадно n/2 секций на ИНУН. Рассматриваются только фильтры четного порядка, поскольку для фильтра нечетного порядка нужно столько же операционных усилителей, сколько и для фильтра на единицу большего порядка. В каждой секции R₁ = R₂ = R и C₁ = С₂ = С. Как и обычно в схемах на операционных усилителях, значение R выбирается в диапазоне от 10 до 100 кОм. (Резисторов с малым номиналом сопротивления лучше избегать, поскольку на высоких частотах возрастающее выходное полное сопротивление разомкнутого контура операционной усилителя добавляется к сопротивлению резистора, внося ошибку в расчет.) Тогда все, что вам нужно сделать - это установить коэффициент усиления каждого каскада K согласно табличным данным. Для n-полюсного фильтра потребуется n/2 обращений к таблице - по числу секций.

Фильтры Баттерворта нижних частот. Если используется фильтр Баттерворта то параметры всех секций имеют одинаковые значения R и С, определяемые соотношением RC = 1/2πƒ_c где ƒ_с - частота, соответствующая значению ослабления всего фильтра, равному -3 дБ. Чтобы построить, например, 6-полюсный фильтр Баттерворта нижних частот, мы соединяем каскадно три вышеописанные секции с коэффициентами усиления, равными соответственно 1,07, 1,59 и 2,48 (желательно именно в указанном порядке, во избежание возни с динамическим диапазоном) и подбором идентичных для всех секций параметров R и С устанавливаем точку, отвечающую значению -3 дБ. Описанная в разд. 8.31 схема управления телескопом представляет собой подобный пример со значением ƒ_с = 88,4 Гц (R = 180 кОм, С = 0,01 мкФ).

Фильтры нижних частот Бесселя и Чебышева. Ненамного сложнее построить на ИНУН фильтр Бесселя или Чебышева. Опять-таки соединим каскадно несколько двухполюсных фильтров на ИНУН с предписанным для каждой секции коэффициентом усиления. Снова в каждой секции зададим R₁ = R₂ = R и С₁ = С₂ = С. Но теперь, в отличие от ситуации с фильтром Баттерворта, произведение RC будет для каждой секции свое и должно выявляться с помощью нормирующего множителя ƒ_n, (его значения для каждой секции приведены в табл. 5.2) по формуле RC = 1/2ƒ_nƒ_c. Здесь через ƒ_с обозначена точка, отвечающая значению -3 дБ, для фильтра Бесселя и граница полосы пропускания - для фильтра Чебышева, т.е. это частота, на которой амплитудно-частотная характеристика спадает ниже диапазона неравномерности при переход6 полосе задерживания. Например, характеристика фильтра Чебышева нижних частот с неравномерностью 0,5 дБ и ƒ_c = 100 Гц будет плоской с небольшой неравномерностью от 0 до -0.5 дБ в диапазоне от 0 до 100 Гц, на частоте 100 Гц будет затухание 0.5 дБ, а дальше частоты 100 Гц - крутой спад. Значения параметров приведены в табл. 5.2 для фильтров Чебышева. имеющих неравномерность характеристики в полосе пропускания 0,5 и 2 дБ - у последнего спад к полосе задерживания несколько круче (рис. 5.17).

Фильтры верхних частот. Чтобы побить фильтр верхних частот, используем показанную ранее конфигурацию фильтра нижних частот, т.е. поменяем местами R и С. При этом для фильтра Баттерворта ничего больше не изменится (значения R, C и K останутся те же). Для фильтров Бесселя и Чебышева сами значения K останутся те же, а нормирующий множитель ƒ_н должен быть обратный, т.е. для каждой секции новое значение равно ƒ_н = 1/ƒ_н (как указано в табл. 5.2).

Полосовой фильтр получается при каскадном соединении фильтров верхних частот и фильтров нижних частот с перекрывающимися полосами пропускания. Полосноподавляющий же фильтр можно получить с помощью схемы сложения выходных сигналов фильтров верхних частот и фильтров нижних частот с неперекрывающимися полосами пропускания. Однако такие каскадные фильтры не очень пригодны там, где нужны фильтры с высокой добротностью (полосовые фильтры с крутой переходной областью) вследствие большой чувствительности индивидуальных (непарных) фильтровых секций к значениям параметров элементов. В таких случаях следует применять высокодобротную однокаскадную полосовую схему (т.е. описанную ранее полосовую схему на ИНУН или рассматриваемые далее биквадратные фильтры и фильтры на основе метода переменных состояния) вместо многокаскадного фильтра. Даже однокаскадный двухполюсный фильтр может иметь характеристику с крайне острым пиком. Информацию о таких конструкциях фильтров можно найти в справочниках.

В фильтрах на ИНУН используется минимальное число элементов (один операционный усилитель на два полюса характеристики), при этом они дают дополнительный выигрыш в виде не инвертирующего коэффициента усиления, низкого выходного полного сопротивления, малого разброса значений параметров, простоты регулировки коэффициента усиления и способности работать при большом коэффициенте усиления или высокой добротности. Их недостаток - высокая чувствительность к изменениям параметров элементов и коэффициента передачи усилителя, кроме того, они не годятся для построения перестраиваемых фильтров с устойчивой характеристикой.

Упражнение 5.3. Спроектируйте на ИНУН 6-полюсный фильтр Чебышева нижних частот с неравномерностью в полосе пропускания 0,5 дБ и среза ƒ_с = 100 Гц. Какое ослабление будет на равной 1,5 ƒ_c?

Генераторы